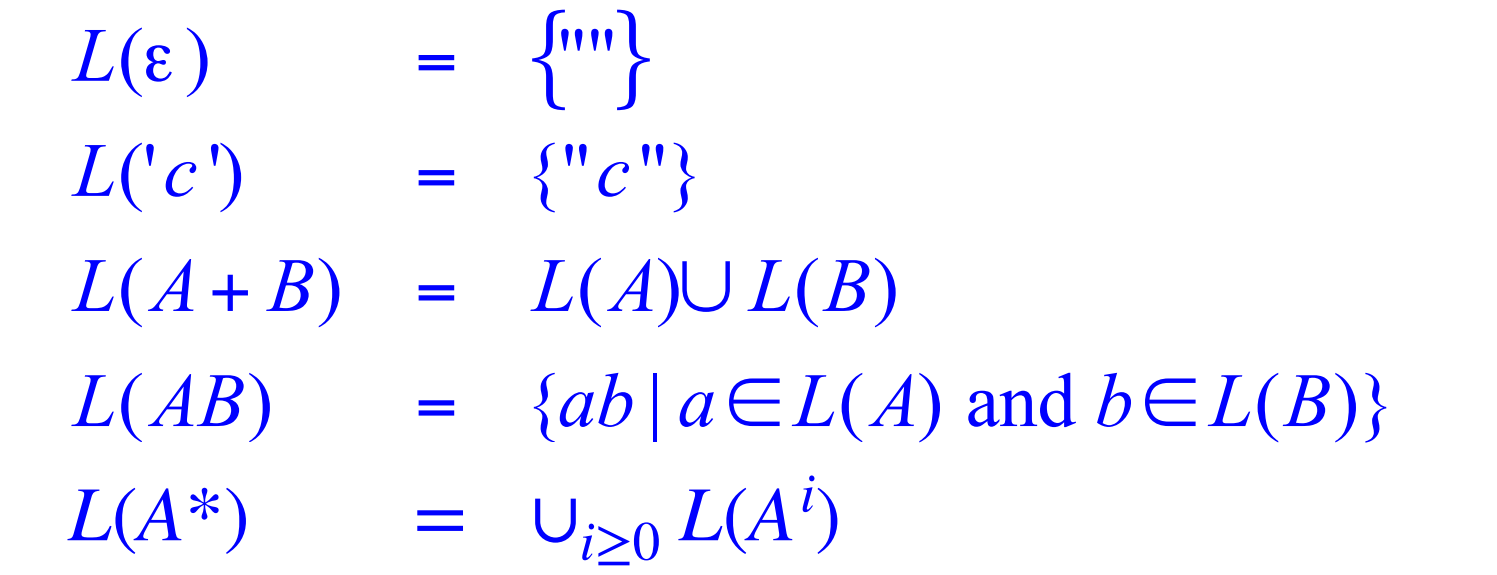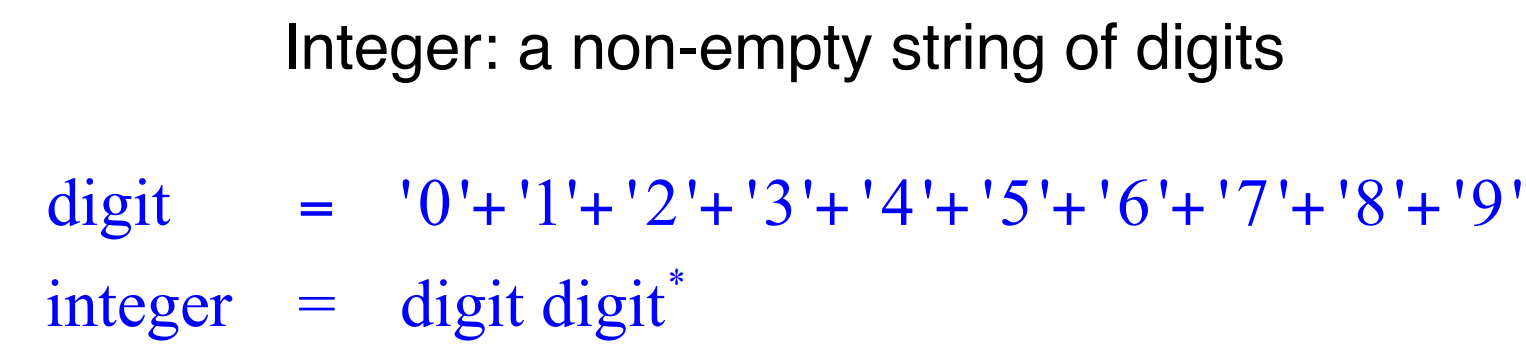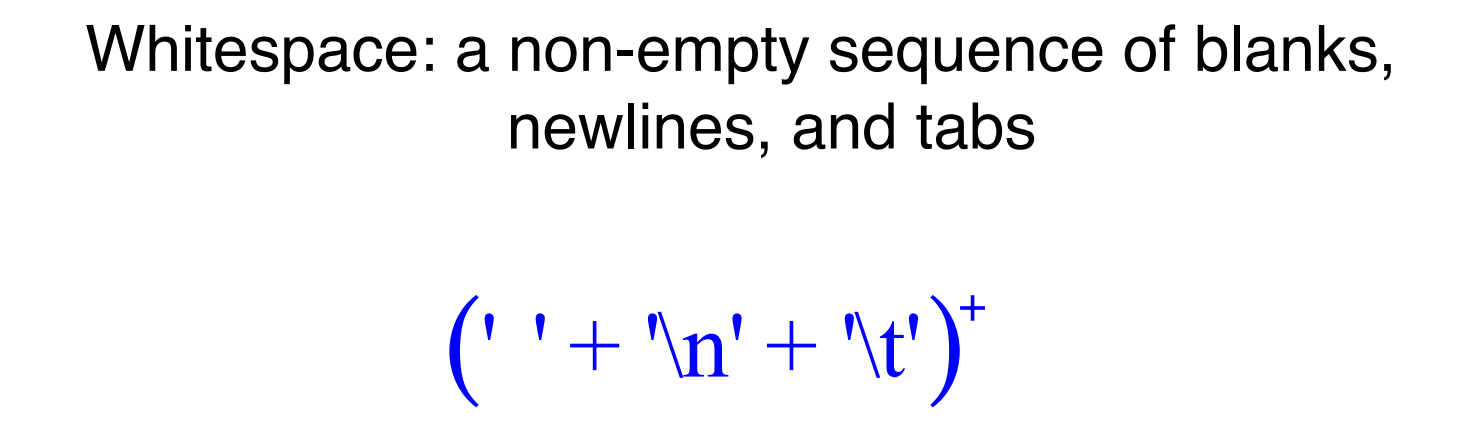CS 143 笔记
Lecture 1
The Structure of a Compiler
- Lexical Analysis —- identify words
- Parsing —- identify sentences
- Semantic Analysis —- analyse sentences
- Optimization —- editing
- Code Generation —- translation
Can be understood by analogy to how humans comprehend English.
- Lexical Analysis First step: recognize words – Smallest unit above letters Lexical analyzer divides program text into “words” or “tokens”
- Parsing Once words are understood, the next step is to understand sentence structure Parsing = Diagramming Sentences - The diagram is a tree

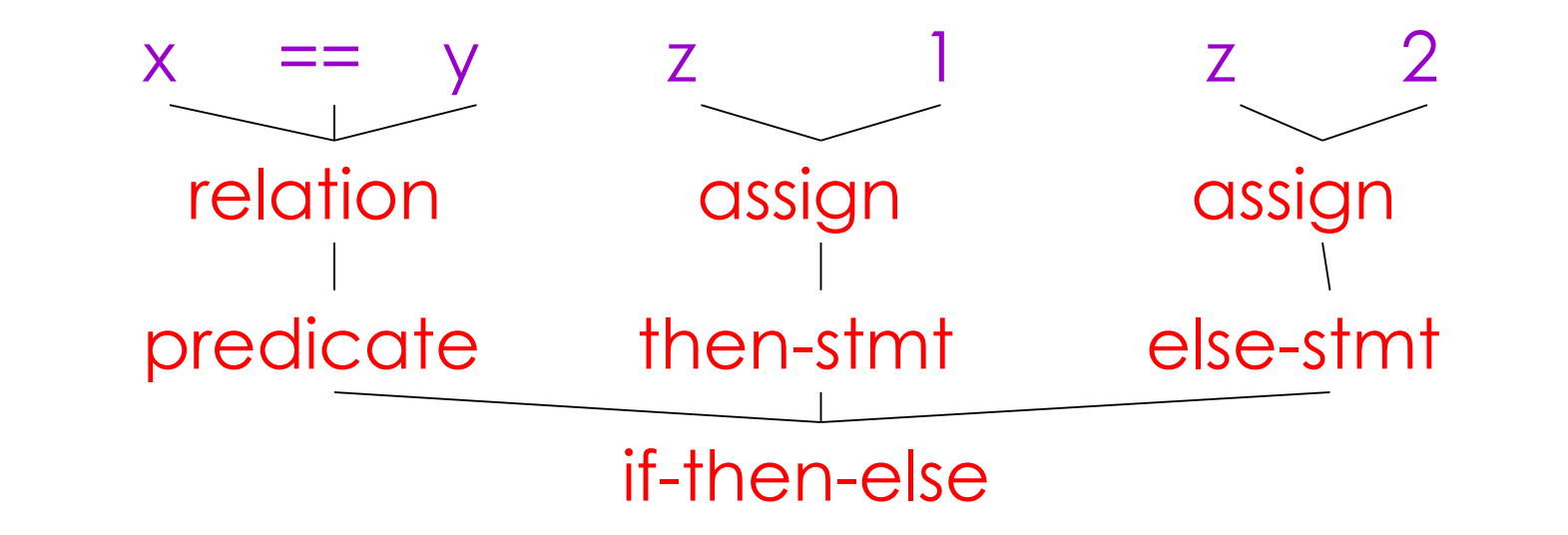
- Semantic Analysis Once sentence structure is understood, we can try to understand “meaning” - But meaning is too hard for compilers Compilers perform limited semantic analysis to catch inconsistencies

 Compilers perform many semantic checks besides variable bindings
Compilers perform many semantic checks besides variable bindings - Optimization Akin to editing - Minimize reading time - Minimize items the reader must keep in short-term memory Automatically modify programs so that they - Run faster - Use less memory - In general, to conserve some resource
- Code Generation Typically produces assembly code Generally a translation into another language - Analogous to human translation
Intermediate Representations
Many compilers perform translations between successive intermediate languages
- All but first and last are intermediate representations (IR) internal to the compiler IRs are generally ordered in descending level of abstraction
- Highest is source
- Lowest is assembly
IRs are useful because lower levels expose features hidden by higher levels
- registers
- memory layout
- raw pointers
- etc
But lower levels obscure high-level meaning
- Classes
- Higher-order functions
- Even loops…
Lecture 2
History of Ideas: Abstraction
- Abstraction = detached from concrete details
- “Abstraction is selective ignorance” - Andrew Koenig
- Abstraction is necessary to build any complex system
- The key is information hiding—expose only the essential
- Modes of abstraction
- Via languages/compilers: High-level code, few machine dependencies
- Via functions and subroutines: Abstract interface to behavior
- Via modules: Export interfaces; hide implementation
- Via classes/abstract data types: Bundle data with its operations
History of Ideas: Types
- Originally, few types
- FORTRAN: scalars, arrays
- LISP: no static type distinctions
- Realization: Types help
- Lets you to express abstraction
- Lets the compiler report many frequent errors
- Sometimes to the point that programs are guaranteed “safe”
- Helps the compiler optimize your code
- More recently
- Lots of interest in types
- Experiments with various forms of parameterization
- Best developed in functional programming
History of Ideas: Reuse
- Reuse = exploit common patterns in software systems
- Goal: mass-produced software components
- Reuse is difficult
- Two popular approaches
- Type parameterization (List(int), List(double))
- Classes and inheritance: C++ derived classes
- C++ and Java have both
- Inheritance allows
- Specialization of existing abstraction
- Extension, modification, and hidden behavior
Lexical Analysis
What do we want to do? Example:
if(i==j)
z=0;
else
z=1;
The input is just a string of characters:
\tif (i == j)\n\t\tz = 0;\n\telse\n\t\tz = 1;
Goal: Partition input string into substrings
- Where the substrings are called tokens
Token
A token class corresponds to a set of strings Examples:
- Identifier: strings of letters or digits, starting with a letter
- Integer: a non-empty string of digits
- Keyword: “else” or “if” or “begin” or
- Whitespace: a non-empty sequence of blanks, newlines, and tabs
Lexical analysis produces a stream of tokens which is input to the parser Parser relies on token distinctions
- An identifier is treated differently than a keyword
Designing a Lexical Analyzer
- Define a finite set of tokens
- Tokens describe all items of interest
- Identifiers, integers, keywords
- Choice of tokens depends on
- language
- design of parser
- Tokens describe all items of interest
Recall
Useful tokens for this expression:
Integer, Keyword, Relation, Identifier, Whitespace, (, ), , ;
- Describe which strings belong to each token Recall:
- Identifier: strings of letters or digits, starting with a letter
- Integer: a non-empty string of digits
- Keyword: “else” or “if” or “begin” or …
- Whitespace: a non-empty sequence of blanks, newlines, and tabs
An implementation must do two things:
- Classify each substring as a token
- Return the value or lexeme (value) of the token
- The lexeme is the actual substring
- From the set of substrings that make up the token The lexer thus returns token-lexeme pairs
- And potentially also line numbers, file names, etc. to improve later error messages
The lexer usually discards “uninteresting” tokens that don’t contribute to parsing
- Examples: Whitespace, Comments
Lexical Analysis in FORTRAN
FORTRAN rule: Whitespace is insignificant
- E.g.,
VAR1is the same asVA R1
Historical footnote: FORTRAN Whitespace rule motivated by inaccuracy of punch card operators
This is a fortran loop. The first token is `Do
This is a assignment. The first toekn is
DO5I
Two important points:
- The goal is to partition the string. This is implemented by reading left-to-right, recognizing one token at a time
- “Lookahead” may be required to decide where one token ends and the next token begins
Lexical Analysis in C++
Unfortunately, the problems continue today C++ template syntax:
Foo<Bar>
C++ stream syntax:
cin >> var;
But there is a conflict with nested templates:
Foo<Bar<Bazz>>
We still need
- A way to describe the lexemes of each token
- A way to resolve ambiguities
- Is if two variables i and f?
- Is == two equal signs = =?
There are several formalisms for specifying tokens Regular languages are the most popular
- Simple and useful theory
- Easy to understand
- Efficient implementations
Def. Let alphabet Σ be a set of characters. A language over Σ is a set of strings of characters drawn from Σ.